Answer:
The % increase in investment after two years is 13.05 %
Explanation:
Given as :
The principal investment = p = $10,000
The rate of interest = r = 6%
The time period t = 1 year
Let The Amount paid after 1 year = $
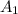
Let The % increase in investment after two years = x
Now, According to question
From Compounded Interest method
Amount = Principal ×

Or,
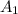 = p ×
= p ×
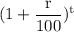
Or,
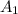 = $10,000 ×
= $10,000 ×
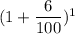
Or,
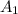 = $10,000 ×
= $10,000 ×
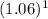
Or,
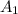 = $10,000 × 1.06
= $10,000 × 1.06
∴
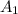 = $10,600
= $10,600
So, The Amount paid after 1 year =
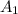 = $10,600
= $10,600
Now, Interest earn = Amount - Principal
Or, I = $10,600 - $10,000
i.e I = $600
So, This interest earn is invested for second year
So, Principal for second year = $10,600 + $600
i.e Principal for second year = $11,200
The rate of interest = r = 7%
The time period t = 1 year
Let The Amount paid after 1 year = $

Now, According to question
From Compounded Interest method
Amount = Principal ×

Or,
 = p ×
= p ×
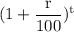
Or,
 = $11,200 ×
= $11,200 ×

Or,
 = $11,200 ×
= $11,200 ×
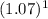
Or,
 = $11,200 × 1.07
= $11,200 × 1.07
∴
 = $11,984
= $11,984
So, The Amount paid after 1 year =
 = $11,984
= $11,984
Now, Again
% increase in investment after two years =
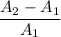 ×100
×100
Or , x =
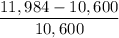 ×100
×100
Or , x =
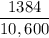 ×100
×100
∴ x = 13.05 %
So, % increase in investment after two years = x = 13.05 %
Hence,The % increase in investment after two years is 13.05 % Answer