Answer:
The number of adult tickets sold is 894 and the number of kid tickets is 750.
Explanation:
Given:
A Six Flags theme park charges $30 for adults and $15 for kids.
Total of 1,644 tickets were sold.
Total amount of tickets $11,250.
Now, to find the number of adult tickets and kid tickets.
Let the number of kid tickets be
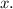
And the number of adult tickets be
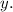
So, the total number of tickets:
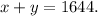 .....(1)
.....(1)
Solving the equation we get the value of
 :
:

Now, the total amount of tickets of adult and kids:
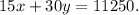
So, by putting the value of
 we get:
we get:
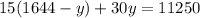

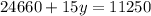
Subtracting both sides by 24660 we get:
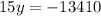
Dividing both sides by -15 we get:
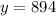
Thus number of adult tickets = 894.
Now, putting the value of
 in equation (1):
in equation (1):

On solving we get:
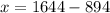
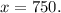
So. the number of kid tickets = 750.
Therefore, the number of adult tickets sold is 894 and the number of kid tickets is 750.