Question

A one-parameter family of solutions of the de p' = p(1 − p) is given below.

P =
c1et
1 + c1et
Does any solution curve pass through the point (0, 4)? Through the point (0, 1)? (If yes, give the corresponding value of

c1.
If not, enter DNE.)

(0, 4) __________
(0, 1) _______________

Answer 1

A solution curve pass through the point (0,4) when
`c_(1) = -(4)/(3)`.

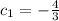There is not a solution curve passing through the point(0,1).

Explanation:

We have the following solution:

`P(t) = (c_(1)e^(t))/(1 + c_(1)e^(t))`

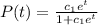
Does any solution curve pass through the point (0, 4)?

We have to see if P = 4 when t = 0.

`P(t) = (c_(1)e^(t))/(1 + c_(1)e^(t))`

`4 = (c_(1))/(1 + c_(1))`

`4 + 4c_(1) = c_(1)`

`c_(1) = -(4)/(3)`

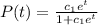
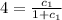
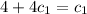
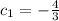
A solution curve pass through the point (0,4) when
`c_(1) = -(4)/(3)`.

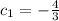Through the point (0, 1)?

Same thing as above

`P(t) = (c_(1)e^(t))/(1 + c_(1)e^(t))`

`1 = (c_(1))/(1 + c_(1))`

`1 + c_(1) = c_(1)`

`0c_(1) = 1`

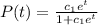
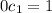
No solution.

So there is not a solution curve passing through the point(0,1).