Question

Is the binomial a factor of the polynomial function?

f(x)=x^3+4x^2−25x−100

(I'm not sure if the highlighted answers are correct, help!!!)

Answer 1

The answers are (x-5) YES (x+2) NO (x-4) NO

Explanation:

I took the test :)

Answer 2

YES

NO

NO

Explanation:

The given polynomial is:
`$ f(x) =  x^3 + 4x^2 - 25x - 100 $`

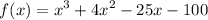
(x - a) is a factor of a polynomial iff x = a is a solution to the polynomial.

To check if (x - 5) is a factor of the polynomial f(x), we substitute x = 5 and check if it satisfies the equation.

∴ f(5) = 5³ + 4(5)² - 25(5) - 100

= 125 + 100 - 125 - 100

= 225 - 225

= 0

We see, x = 5 satisfies f(x). So, (x - 5) is a factor to the polynomial.

Now, to check (x + 2) is a factor.

i.e., to check x = - 2 satisfies f(x) or not.

f(-2) = (-2)³ + 4(-2)² - 25(-2) - 100

= -8 + 16 + 50 - 100

= -108 + 66

≠ 0

Therefore, (x + 2) is not a factor of f(x).

To check (x - 4) is a factor.

∴ f(4) = 4³ + 4(4)² - 25(4) - 100

= 64 + 64 - 100 - 100

= 128 - 200

≠ 0

Therefore, (x - 4) is not a factor of f(x).