Answer:
see the explanation
Explanation:
we know that
As the leading coefficient of the quadratic equation gets larger the parabola gets steeper and "narrower"
we have
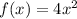
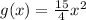
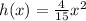
Compare the leading coefficients
The leading coefficient of f(x) is 4
The leading coefficient of g(x) is 15/4=3.75
The leading coefficient of h(x) is 4/15=0.27
so
4> 3.75> 0.27
therefore
f(x) is steeper than g(x) and h(x)
g(x) is steeper than h(x)
Verify each statement
1) f(x) is steeper than h(x)
The statement is true
2) h(x) is steeper than g(x)
The statement is false
3) g(x) is steeper than f(x)
The statement is false