Answer:
The fundamental theorem of algebra guarantees that a polynomial equation has the same number of complex roots as its degree.
Explanation:
The fundamental theorem of algebra guarantees that a polynomial equation has the same number of complex roots as its degree.
We have to find the roots of this given equation.
If a quadratic equation is of the form
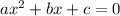
Its roots are
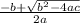 and
and
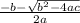
Here the given equation is
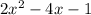 = 0
= 0
a = 2
b = -4
c = -1
If the roots are
 , then
, then
 =
=
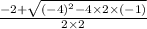
=
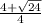
=
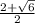
 =
=
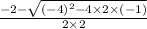
=
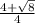
=

These are the two roots of the equation.