Question

Computer Help Hot Line receives, on average, 14 calls per hour asking for assistance. Assume the variable follows a Poisson distribution. What is the probability that the company will receive more than 20 calls per hour? Round answer to 4 decimal places.

Answer 1

Answer: 0.0479

Explanation:

Given : Computer Help Hot Line receives, on average, 14 calls per hour asking for assistance.

Let x be number of variable that denotes the number of calls that follows a Poisson distribution.

Poisson distribution formula :
`P(X=x)=(e^(-\lambda)\lambda^x)/(x!)`

, where
`\lambda` =Mean of the distribution.

Here ,

Then, the probability that the company will receive more than 20 calls per hour=
`P(x>20)=1-P(x\leq20)`

`=1-0.9521=0.0479`

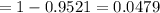
(From Cumulative Poisson distribution table the value of P(x ≤ 20) =0.9521 corresponding to
`\lambda=14` ).

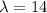Thus , the probability that the company will receive more than 20 calls per hour = 0.0479