Question

Y-3=3(x+1)

what is the equation in standard form of a perpendicular line that passes through (5,-1)

Answer 1

Answer: x + 3y = 2

Explanation:

Given:

y - 3 = 3 ( x + 1 )

y - 3 = 3x + 3

y = 3x + 3 + 3

y = 3x +6

comparing the equation with the formula for finding equation of line in slope - intercept form

y = mx + c , where m is the slope and c is the y - intercept. This means that the slope of the line above is 3

Two lines are said to be perpendicular if the product of their slope = -1, that is , if
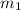`m_(1)` is the slope of the first line and
`m_(2)` is the slope of the second line , if they are perpendicular , then
`m_(1)`
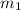
`m_(2)` = -1

Considering this rule , this means that the slope of the line we are to find =
`(-1)/(3)`

Using the formula : y -
`y_(1)` = m ( x -
`x_(1)` ) to find the equation of the line , we have

y - (-1 ) =
`(-1)/(3)` ( x - 5 )

y + 1 =
`(-1)/(3)` ( x - 5 )

multiplying through by 3 , we have

3 ( y + 1 ) = -1 ( x - 5)

Expanding , we have

3y + 3 = -x + 5

writing the equation in standard form , we have

3y + x = 5 - 3

Therefore :

x + 3y = 2