Question

Here’s another one if you want to answer it

Answer 1

D.
`(-9)/(2) \leqx <(27)/(2)`

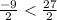
Step-by-step explanation:

Before proceeding, please remember the following:

1. When you do a certain operation on one side of the inequality, you have to do the same operation on ALL other sides to keep the original value of the inequality unchanged

2. To solve an inequality means that we want to isolate the variable.

Now, for the given inequality, we have:

`-3 \leq(2x-3)/(4) <6`

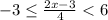
Based on the above, for the middle part of the inequality, we want to have the x variable standing alone.

This can be done as follows:

1. Multiply all sides by 4

This would give us:
`-12 \leq 2x-3 < 24`

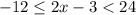
2- Add 3 to all sides

This would give us:
`-9 \leq2x < 27`

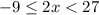
3- Finally, divide all sides by 2 to have the x on its own

This would give us:
`(-9)/(2) \leq x < (27)/(2)`

Hope this helps :)