Question

A gun with a muzzle velocity of 1500 feet per second is fired at an angle of 6 degrees with the horizontal. Find the vertical and horizontal components of the velocity to the nearest whole number.

Answer 1

The vertical component of velocity is 156 feet per second

The horizontal component of velocity 1491 feet per second .

Explanation:

Given as :

The velocity of gun = v = 1500 feet per sec

The angle made by gun with horizontal = Ф = 6°

Let The vertical component of velocity =
`v__y`

Let The horizontal component of velocity =
`v__x`

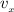
Now, According to question

The vertical component of velocity = v sin Ф

i.e
`v__y` = v sin Ф

Or ,
`v__y` = 1500 ft/sec × sin 6°

Or ,
`v__y` = 1500 ft/sec × 0.104

∴
`v__y` = 156 feet per second

So, The vertical component of velocity =
`v__y` = 156 feet per second

Now, Again

The horizontal component of velocity = v cos Ф

i.e
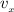`v__x` = v cos Ф

Or ,
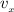`v__x` = 1500 ft/sec × cos 6°

Or ,
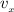`v__x` = 1500 ft/sec × 0.994

∴
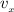`v__x` = 1491 feet per second

So, The horizontal component of velocity =
`v__y` = 1491 feet per second

Hence,The vertical component of velocity is 156 feet per second

And The horizontal component of velocity 1491 feet per second . Answer