Question

Find the indicated term of the geometric sequence. a8 for 4, -12, 36, ...

Answer 1

76

Explanation:

Answer 2

The 8th term of geometric sequence is -8748

ie.,
`a_(8)=-8748`

Explanation:

Given geometric sequence is 4,-12,36,...

Geometric sequence can be written as

`a_(1),a_(2),a_(3),..,`

`a_(1)=4=a`

`a_(2)=-12=ar`

`a_(3)=36=ar^2`

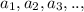
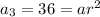
and so on.

common ratio is
`r=(a_(2))/(a_(1))`

`r=(-12)/(4)`

`r=-3`

`r=(a_(3))/(a_(2))`

`r=(36)/(-12)`

`r=-3`

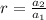
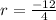
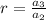
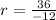
Therefore
`r=-3`

Geometric sequence of nth term is
`a_(n)=ar^(n-1)`

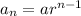
To find the 8th term:

`a_(8)=ar^(8-1)`

`a_(8)=ar^(7)`

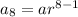
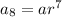
here a=4 and r=-3

`a_(8)=ar^(7)`

`=4* (-3)^7`

`=4* (-2187)`

`=-8748`

`a_(8)=-8748`

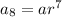
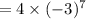
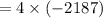
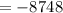
Therefore the 8th term of geometric sequence is -8748