Question

(3 points)

11. A farmer buys 20 sheep, half male and half female. She was told that the annual rate of
increase for the sheep population is 60%. Assuming that none of the sheep die, when will the
farmer have 200 sheep? Write and solve an exponential equation, showing your work.
Use
to indicate an exponent. Use /to indicate a fraction.

Answer 1

The exponential Function is
`20+12h=200`.

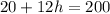Farmer will have 200 sheep after 15 years.

Explanation:

Given:

Number of sheep bought = 20

Annual Rate of increase in sheep = 60%

We need to find that after how many years the farmer will have 200 sheep.

Let the number of years be 'h'

First we will find the Number of sheep increase in 1 year.

Number of sheep increase in 1 year is equal to Annual Rate of increase in sheep multiplied by Number of sheep bought and then divide by 100.

framing in equation form we get;

Number of sheep increase in 1 year =
`(60)/(100)*20 = 12`

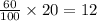
Now we know that the number of years farmer will have 200 sheep can be calculated by Number of sheep bought plus Number of sheep increase in 1 year multiplied by number of years is equal to 200.

Framing in equation form we get;

`20+12h=200`

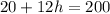
The exponential Function is
`20+12h=200`.

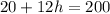Subtracting both side by 20 using subtraction property we get;

`20+12h-20=200-20\\\\12h=180`

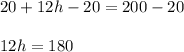
Now Dividing both side by 12 using Division property we get;

`(12h)/(12) = (180)/(12)\\\\h =15`

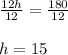
Hence Farmer will have 200 sheep after 15 years.