Question

Using the dot plots provided, what is the mean absolute deviation of the height of basketball players, rounded to the nearest tenth?

Answer 1

`MAD= (1)/(14) 27.286 = 1.949 \approx 2.0`

Explanation:

Previous concepts

The mean absolute deviation or MAD "is the average of the absolute deviations or the positive difference of the given data and that certain value (generally central values)". And is given by this formula:

`MAD= (1)/(n) \sum_(i=1)^n |x_i -\bar X|`

Solution to the problem

Assuming the info from the picture. So then the data is this one:

66,69,70,70,71,72,72,72,73,73,74,75,75,75

So the first step is find the mean for the dataset with the following formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

And if we replace the values we got:

`\bar X = (66+69+70+70+71+72+72+72+73+73+74+75+75+75 </p><p>)/(14)=71.929`

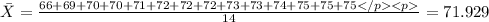
And now we need to subtract for each value the mean like this:

Data
`X_i -\bar X`

66 5.929

69 2.929

70 1.929

70 1.929

71 0.929

72 0.0714

72 0.0714

72 0.0714

73 1.0714

73 1.0714

74 2.0714

75 3.0714

75 3.0714

75 3.0714

Now we need to add the deviations and divide by the the number of data values and we got:

`MAD= (1)/(14) 27.286 = 1.949 \approx 2.0`