Answer:
11 positive integers can be expressed.
Explanation:
Consider the provided information.
The number of possible prime numbers are 5,7,11,and 13.
There are 4 possible prime numbers.
How many positive integers can be expressed as a product of two or more of the prime numbers, that means there can be product of two numbers, three number or four numbers.
The formula to calculate combinations is:
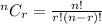
The number of ways are:


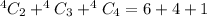

Hence, 11 positive integers can be expressed.