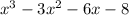Answer:
With the given zeros x=-2,1,4 the polynomial function is
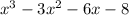
Explanation:
Given zeros are x=-2,1,4
Now to find the polynomial function:
With the given zeros we can write it as below:
x=-2 implies that x+2=0
x=-1 implies that x-1=0
x=4 implies that x-4=0
Then we can the zeros or factors by (x+2)(x-1)(x-4)
Now expanding the zeros or factors:

 ( multiply each term with each term of another factor)
( multiply each term with each term of another factor)
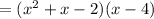 ( adding the like terms)
( adding the like terms)
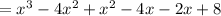 ( multiply each term with each term of another factor)
( multiply each term with each term of another factor)
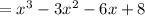 ( adding the like terms)
( adding the like terms)
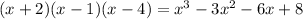
Therefore the polynomial function is
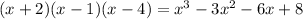
With the given zeros x=-2,1,4 the polynomial function is