If dy/dx = xy2 and x = 1 when y = 1, then y = Your answer: 0 x2 o — 2 2 3 Q x2 - 3 22 +1 2–3 2

Question

asked Sep 7, 2023 171k views

2 Answers

Adriaan Davel · Answer 1 · 2023-09-13T13:38:31+0000

Let's first start with the given that we have ;

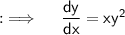
${:\implies \quad \sf (dy)/(dx)=xy^(2)}$

Collect like terms in different sides ;

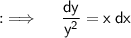
${:\implies \quad \sf (dy)/(y^2)=x\: dx}$

Integrating both sides will yield

${:\implies \quad \displaystyle \sf \int y^(-2)dy=\int x^(1)dx}$

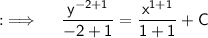
${:\implies \quad \sf (y^(-2+1))/(-2+1)=(x^(1+1))/(1+1)+C}$

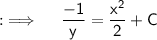
${:\implies \quad \sf (-1)/(y)=(x^2)/(2)+C}$

Where, C is the Arbitrary Constant;

Now, as we are given that x becomes 1, when y = 1, so putting these values we will obtain C = (-3/2) , putting the values ;

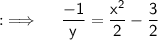
${:\implies \quad \sf (-1)/(y)=(x^2)/(2)-\frac32}$

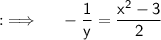
${:\implies \quad \sf -(1)/(y)=(x^(2)-3)/(2)}$

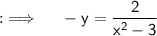
${:\implies \quad \sf -y=(2)/(x^(2)-3)}$

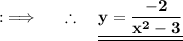
${:\implies \quad \bf \therefore \quad \underline{\underline{y=(-2)/(x^(2)-3)}}}$

Option B) is the required answer