Answer: 0.0001
Explanation:
Given : For women aged 18-24, systolic blood pressures (in mm Hg) are normally distributed with a mean of 114.8 and a standard deviation of 13.1.
i.e.
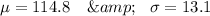
Sample size =4
Let x be the sample mean systolic blood pressure.
Then the probability that their mean systolic blood pressure is greater than 140 will be
![P(x>140)=1-P(x\leq140)\\\\=1-P((x-\mu)/((\sigma)/(√(n)))\leq(140-114.8)/((13.1)/(√(4))))\\\\\ =1-P(z\leq3.85)\ \ [\because \ z=(x-\mu)/((\sigma)/(√(n)))]\\\\=1-0.9999\ \ \text{[By z-table]}\\\\= 0.0001](https://img.qammunity.org/2021/formulas/mathematics/high-school/382f0e7iloket4wmsd6fazaxi4zgi9pyyl.png)
Hence, the required probability = 0.0001