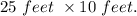Question

Mr. Johnson currently has a square garden. It is in his garden and into a range of 5 feet shorter than three times shorter than times it width. He decides that the perimeter should be 70 feet. Determine the dimensions, in feet, of his new garden

Answer 1

The Dimension of new garden is
`25 \ feet\ * 10\ feet.`

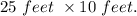
Explanation:

Given:

Perimeter of new garden = 70 feet.

Let the length of the new garden be 'l'.

Also Let the width of the new garden be 'w'.

We need to find the dimension of new garden.

Now Given:

Length is 5 feet shorter than three times it width.

framing the equation we get;

`l =3w-5 \ \ \ \ equation\ 1`

Now we know that;

Perimeter of rectangle is equal to twice the sum of length and width.

framing in equation form we get;

`2(l+w)=70`

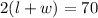
Now Diving both side by 2 using Division property of equality we get;

`\frac{2(l+w)}2=(70)/(2)\\\\l+w =35`

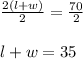
Now Substituting equation 1 in above equation we get;

`3w-5+w=35\\\\4w-5=35`

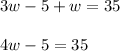
Adding both side by 5 Using Addition Property of equality we get'

`4w-5+5=35+5\\\\4w=40`

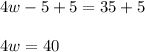
Now Diving both side by 4 using Division property of equality we get;

`(4w)/(4)=(40)/(4)\\\\w=10\ ft`

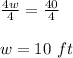
Now Substituting the value of 'w' in equation 1 we get;

`l =3w-5\\\\l =3*10-5\\\\l = 30-5\\\\l= 25\ ft`

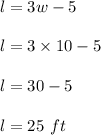
Hence The Dimension of new garden is
`25 \ feet\ * 10\ feet.`