Question

Solve the triangle. B = 73°, b = 15, c = 10

Answer 1

Incomplete Question, the complete question is

Solve the triangle.

B = 73°, b = 15, c = 10

A. C = 39.6°, A = 67.4°, a ≈ 14.5

B. Cannot be solved

C. C = 44.8°, A = 62.4°, a ≈ 14.5

D. C = 39.6°, A = 67.4°, a ≈ 20.3

Answer:

The Answer is the option A

A. C = 39.6°, A = 67.4°, a ≈ 14.5

Explanation:

Given:

In Δ ABC,

∠B = 73°

b = 15

c = 10

To Find:

∠A = ?

∠B = ?

a = ?

Solution:

IN Δ ABC, Sine Rule says that

`(a)/(\sin A)= (b)/(\sin B)= (c)/(\sin C)`

Substituting the given values we get

`(15)/(\sin 73)= (10)/(\sin C)\\\\\sin C=0.6375\\\therefore C=39.6\°`

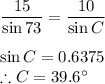
Triangle sum property:

In a Triangle sum of the measures of all the angles of a triangle is 180°.

`\angle A+\angle B+\angle C=180\\\\73+39.6+\angle A=180\\\therefore m\angle A =180-112.6=67.4\°`

∴
`(a)/(\sin A)= (b)/(\sin B)`

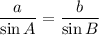
Substituting the given values we get

∴
`(a)/(\sin 67.4)= (15)/(\sin 73)\\\\\therefore a=14.48\approx14.5`

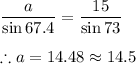
Therefore,

A. ∠C = 39.6°, ∠A = 67.4°, a ≈ 14.5