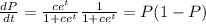Answer:
See verification below
Explanation:
We can differentiate P(t) respect to t with usual rules (quotient, exponential, and sum) and rearrange the result. First, note that
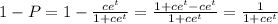
Now, differentiate to obtain
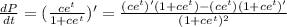
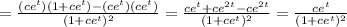
To obtain the required form, extract a factor in both the numerator and denominator: