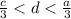Question

There are three different hoses used to fill a pool: hose x, hose y, and hose z. Hose x can fill the pool in a days, hose y in b days, and hose z in c days, where a > b > c. When all three hoses are used together to fill a pool, it takes d days to fill the pool. Which of the following must be true?I. dbIII. c/3

Answer 1

C) I and III only

Explanation:

Let full pool is denoted by O

Days Hose x takes to fill pool O = a

Pool filled in one day x = O/a

Days Hose y takes to fill pool O = b

Pool filled in one day y = O/b

Days Hose z takes to fill pool O = c

Pool filled in one day z = O/c

It is given that

a>b>c

`a>b>c>d\\\implies x<y<z<(x+y+z)\\`

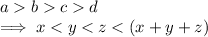
Days if if x+y+z fill the pool together = d

1 day if x+y+z fill the pool together
`=O((1)/(a)+(1)/(b)+(1)/(c))=(O)/(d)---(1)`

I) d < c

d are days when hose x, y, z are used together where as c are days when only z is used so number of days when three hoses are used together must be less than c when only z hose is used. So d < c

III)
`(c)/(3)<d<(a)/(3)`

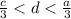
Using (1)

`(bc+ac+ab)/(abc)=(1)/(d)\\\\d=(abc)/(ab+bc+ca)\\\\As\quad(a>b>c)\\(ab+bc+ca)<3ab\\\\d=(abc)/(ab+bc+ca)>(abc)/(3ab)\\\\d>(c)/(3)`

Similarly

`(bc+ac+ab)/(abc)=(1)/(d)\\\\d=(abc)/(ab+bc+ca)\\\\As\quad a>b>c\\(ab+bc+ca)>3bc\\\\d=(abc)/(ab+bc+ca)<(abc)/(3bc)\\\\d<(a)/(3)`

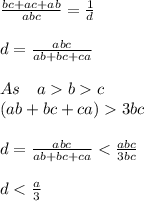
So,

`(c)/(3)<d<(a)/(3)`