Question

Select the correct answer from the drop-down menu.

Phoebe runs a T-shirt printing business. She ships the T-shirts to retailers in boxes of 200. She has two automated printing machines that can
print designs on T-shirts. One machine can print 200 T-shirts in 50 minutes. The other machine can print 200 T-shirts in 150 minutes.
If the two machines work at the same time, they can print 200 T-shirts in
minutes.

Answer 1

Answer:
37.5 Minutes
Explanation:

1. I set up the fourmula: 1/50 + 1/150 = 1/x

2. I rewrote the fractions with a denominator which was 750 in this case: 50/750 + 150/750 = 1/x

3. I added the numerators: 200/750 = 1/x

4. I took the reciprocal of both sides of the equation: 750/200 = x/1

5. I wrote the result as a decimal number: 3.75 ≈ 37.5 minutes.

So, they can print 200 T-shirts in 37.5 minutes.

Answer 2

They will work together and print 200 T-shirts in 37.5 minutes.

Explanation:

One machine can print 200 T-shirts in 50 minutes.

So, in one minute that machine can print
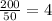`(200)/(50) = 4` T-shirts.

Again, the other machine can print 200 T-shirts in 150 minutes.

So, in one minute the other machine can print
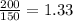`(200)/(150) = 1.33` T-shirts.

Therefore, working together for one minute both the machines will print (4 + 1.33) = 5.33 number of T-shirts.

Hence, they will work together and print 200 T-shirts in
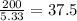`(200)/(5.33) = 37.5` minutes. (Answer)