Question

MNOP is a parallelogram. U is any point on side OP. Show that ar( MUN)= ar ( Δ △ PUM)+ar( UNO) △

Answer 1

The Proof is below.

Explanation:

Given:

[]MNOP is a Parallelogram

U is any point on side OP

To Show:

ar(Δ MUN)= ar ( Δ PUM)+ar (Δ UNO)

Proof:

Theorem:

If a triangle and parallelogram are on the same base and have the same altitude, the area of the triangle will be half that of the parallelogram.

If they have same altitude, they will lie between the same parallels.

Hence the area of the triangle will be equal to half that of the parallelogram.

Area of Parallelogram will be twice of Area of Triangle

∴
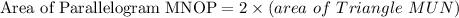`\textrm{Area of Parallelogram MNOP}=2* (area\ of\ Triangle\ MUN)`.............( 1 )

Also,

`\textrm{Area of Parallelogram MNOP}=Ar(MUN) + Ar(PUM)+ Ar(UNO)`

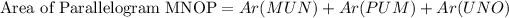
Substituting equation 1 we get

`2* Ar(MUN)=Ar(MUN) + Ar(PUM)+ Ar(UNO)`

`2* Ar(MUN)-Ar(MUN) = Ar(PUM)+ Ar(UNO)`

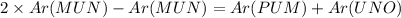
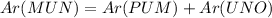`Ar(MUN) = Ar(PUM)+ Ar(UNO)`...........Proved