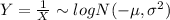Question

Suppose that X has the lognormal distribution with parameters μ and σ2. Find the distribution of 1/X.

Answer 1

`(1)/(X) \sim log N(-\mu , \sigma^2)`

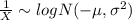
Explanation:

For this case we know that the distribution for the random variable is given by:

`X \sim logN(\mu ,\sigma^2)`

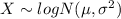
The density function for the log normal random variable is given by:

`f)x,\sigma) = (1)/(x \sigma √(2\pi))e^{- (ln x^2)/(2\sigma^2)}`

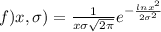
And we want to find the distribution for the random variable
`(1)/(X)`

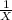
In order to find this distribution we can use the cumulative distribution function like this:

Let
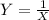`Y= (1)/(X)`, if we solve for X from this transformation we got:

`X= (1)/(Y)`

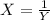
And then we have this:

`F_Y (y) = P(Y \leq y) = P(X \leq (1)/(y)) = F_X ((1)/(y))`

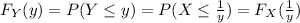
And we can find the density function as the derivate of the distribution function like this:

`f_Y (y) = F'_Y (y) = -(1)/(y^2) f_Y((1)/(y))`

`f_Y (y)= -(1)/(y^2) (1)/((1)/(y) \sigma √(2\pi)) e^{- (ln((1)/(y))^2)/(2\sigma^2)}`

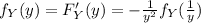
But we see that we don't have an specified form for the distribution

If we assume that X follows a normal distribution
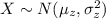`X\sim N (\mu_z,\sigma^2_z)` and we use the transformation
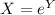`X=e^Y` we see that X follows a log normal distribution. And we see that:

`(1)/(X)= (1)/(e^Y)=e^(-Y)`

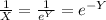
And if we find the distribution of
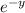`e^(-y)` we got this:

`f_Y (y) = F'_Y (y) = -e^(-y) f_Y(e^(-y))`

`f_Y (y)= -e^(-y) (1)/(e^(-y) \sigma √(2\pi)) e^{- (ln(e^(-y))^2)/(2\sigma^2)}`

`f_Y (y) = -(1)/(\sigma √(2\pi))e^{(y^2)/(2\sigma^2)}`

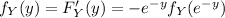
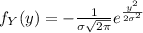
And then we see that
`Y= (1)/(X) \sim log N(-\mu , \sigma^2)`