Answer:
a) 4.40 s
b) 2.20 s
Step-by-step explanation:
Given parameters are:
At constant power ,
initial speed of the car,

final speed of the car,
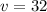 mph
mph
At full power,
initial speed of the car,

final speed of the car,
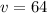 mph
mph
a)
At constant power,
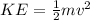
At full power,
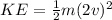
So
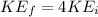
So, time to reach 64 mph speed is 4 times more than the initial time
 s
s
b)
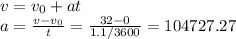
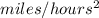
For final 64 mph speed,
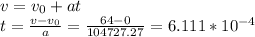
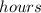 =
=
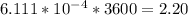 s
s