Question

Find the odds for and the odds against the event rolling a fair die and getting a 1, a 4,or a 5

Answer 1

Odds for = Odds against = 1/2

Explanation:

In a fair die, we have {1, 2, 3, 4, 5, 6} and
`$ n(S) = 6 $`

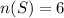
{1, 4, 5} and {2, 3, 6} constitute the entire sample space.

So, Probability of getting a 1 or a 4 or a 5

= Probability of getting a 1 +

Probability of getting a 4 +

Probability of getting a 5

=
`$ (1)/(6) + (1)/(6) + (1)/(6) $`

=
`$ (3)/(6) = (1)/(2) $`

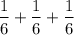
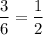
Therefore, Odds for 1 or 4 or 5 =
`$ (1)/(2) $`.

Since, Probability of getting a number between 1 and 6 is 1 and Probability of getting a number from 2 or 3 or 6 =
`$ (1)/(2) $`, we have:

Probability of not getting a 1 or 4 or 5 = 1 -
`$ (1)/(2) $`

=
`$ (1)/(2) $`

Hence, odds for and odds against =
`$ (1)/(2) $`