Question

ABCD is a quadrilateral-shaped field in which diagnol BD is 36m, AL perpendicular to BD and CM perpendicular to BD such that AL=19m and CM=11m. Find the area of the field

Answer 1

Area of the field is 540 m².

Explanation:

ABCD is the given quadrilateral in which diagonal BD is 36 m.

Now, AL ⊥ BD and CM ⊥ BD. Also, AL = 19 m and CM = 11 m.

Now, we have to calculate the area of quadrilateral shaped field ABCD.

At first, we will find the area of ΔABD and ΔBCD and then we will add the area of both the triangles to get the area of the quadrilateral shaped field.

Now, ΔABD and ΔBCD are both right angled triangles.

So,

`area\; of \; triangle \; ABD = (1)/(2) * base* height`

`=(1)/(2)* BD* AL=(1)/(2)*36*19=342\; m^(2)`

`area \; of \; triangle\; BCD = (1)/(2)* BD* CM=(1)/(2)*36* 11 = 198\; m^(2)`

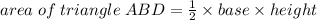
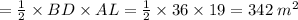
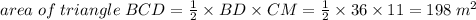
So, area of field ABCD = area of ΔABD + area of ΔCBD

= 342 + 198

= 540 m²

So, the area of quadrilateral shaped field is 540 m².