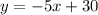Answer:
1.

2.
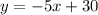
Explanation:
Preliminary Material:
A line that is perpendicular to another has the opposite reciprocal slope of the other line.
- Ex:
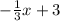 is perpendicular to
is perpendicular to
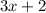 because
because
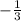 is an opposite reciprocal to
is an opposite reciprocal to
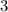 .
.
A line parallel to another has the same slope.
With this in mind, we can begin to answer this question.
1.
Setup for question 1:
A line perpendicular with
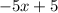 that goes through the point (7, 5).
that goes through the point (7, 5).
Before going over the point this perpendicular line must go through, let's make an equation with the slope of the perpendicular line.
A linear function can be represented with this formula:
 .
.
 = the slope of the line.
= the slope of the line.- b = the y intercept.
We know the slope of this function must be an opposite reciprocal to -5, and using the information I first gave in the beginning of this problem, we can have the slope of the function.
- the opposite reciprocal of
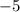 (or
(or
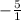 ) is
) is
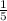 .
.
If we take this slope and insert it into the linear equation, we will have the function...
So we now know the slope of this function, but what about the y intercept,
 ? This is where the point given to us in the beginning of this problem comes into play. If we plug the point (7, -5) into our x and y coordinates in the above equation, we can solve for
? This is where the point given to us in the beginning of this problem comes into play. If we plug the point (7, -5) into our x and y coordinates in the above equation, we can solve for
 .
.
Algebra:

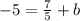
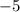 is the same as the fraction
is the same as the fraction
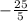 .
.
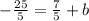
- subtract
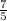 from both sides.
from both sides.
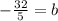
 is equal to
is equal to
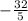 or
or
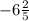 . Lets plug this into our original equation, and we're done.
. Lets plug this into our original equation, and we're done.
Answer:
Our final answer is:
 .
.
2.
There will be no setup for 2. I'll show the algebra without explanation as well. If there's any confusion you can ask me :).
Algebra:

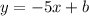
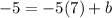


Answer:
- Our final answer is: