Answer:
the correct option is D.
Explanation:
x+3y>6
y≥2x+4
consider the equation x+3y=6
3y = 6-x
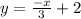
this line is in the form of y = mx + c
where m is the slope os the line and c is the y intercept of the line
therefore the line has a y intercept of 2 and slope of-1/3
therefore the line has negative slope with positive intercept.
now consider the line y=2x+4
this line is in the form of y = mx + c
where m is the slope os the line and c is the y intercept of the line
therefore slope = 2 and y intercept = 4
therefore the line has positive slope and positive y intercept.
in option a both line has positive intercept so it cant be an answer.
in option b one line has positive intercept of 2 and another with negative intercept of -4 but we need intercept of both line to be positive so it cant be an answer.
in option c both line has negative intercept of -2 and -4 but we need intercept of both line to be positive so it cant be an answer.
in option d both line has positive intercept of 2 and 4 and also one of the line has negative slope and another line has positive slope so it should be an answer
further to confirm consider x+3y>6
put the point 0,0 in the inequality
0>6 which is wrong so 0,0 cant lie in the region which is true according to the graph.