Question

The solution to a system of linear equations is (-3,-3). Which system of linear equations has this point as its solution?

x-5y = -12 and 3x+2y = -15
OX-5y=-12 and 3x+2y = 15
x-5y = 12 and 3x+2y = - 15
X-5y = 12 and 3x + 2y = 15​

Answer 1

Option c) is correct.

That is x-5y=12 and 3x+2y=-15 are the system of linear equations satisfies the point (-3,3) so this is the solution.

Explanation:

To verify that which system of linear equations having the solution (-3,-3)

Let
`x-5y=12\hfill (1)`

and
`3x+2y=-15\hfill (2)`

To solve it we have to use elimination method

First multiply the equation(1) into 3 we get

`3x-15y=36\hfill (3)`

Now subtracting the equations (2)and (3) the signs may vary in the second equation we get

`3x-15y=36`

`-3x-2y=+15`

________________

`-17y=51`

_______________

`y=-(51)/(17)`

`y=-3`

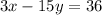
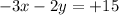
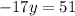
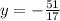
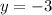
Now substitue the value y=-3 in equation (1) we get

`x-5y=12`

`x-5(-3)=12`

`x=12-15`

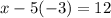
Therefore x=-3

Therefore the solution is (-3,-3)

Therefore Option c) is correct.

That is x-5y=12 and 3x+2y=-15 are the system of linear equations satisfies the point (-3,3) so the solution is (-3,-3).