Question

Find the seventh term of an increasing geometric progression if the first term is equal to 9−4sqrt5 and each term (starting with the second) is equal to the difference of the term following it and the term preceding it.

Answer 1

7th term = 1.

Explanation:

Given that, first term of increasing geometric progression is 9-4√5.

each term (starting with the second) is equal to the difference of the term following it and the term preceding it.

let first term of geometric progression be a and the increasing ratio be r.

⇒ The geometric progression is a , ar , ar² , ar³, ....... so on.

Given, each term (starting with the second) is equal to the difference of the term following it and the term preceding it.

⇒ second term = (third term - first term)

⇒ ar = (ar² - a)

⇒ r = r² - 1

⇒ r² - r -1 =0

⇒ roots of this equation is r =
`(1+√(5) )/(2)` ,
`(1-√(5) )/(2)`

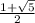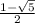
(roots of ax²+bx+c are
`\frac{-b+\sqrt{b^(2) -4ac} }{2a}` and
`\frac{-b-\sqrt{b^(2) -4ac} }{2a}`)

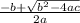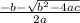and it is given, increasing geometric progression

⇒ r > 0.

⇒ r =
`(1+√(5) )/(2)`.

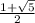Now, nth term in geometric progression is arⁿ⁻¹.

⇒ 7th term = ar⁷⁻¹ = ar⁶.

= (9-4√5)(
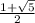`(1+√(5) )/(2)`)⁶

= (0.05572809)(17.94427191) = 1

⇒ 7th term = 1.