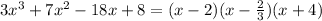Answer:
The factors are x-2,
 and x+4
and x+4
Therefore the expression can be written as
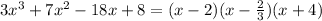
Explanation:
Given expression is
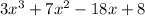
And also given that x-1 is one of the factors
i.e.,x-1=0
x=1
To find the factors equate the given expression to zero
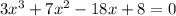
Using synthetic division to find the factors
1_| 3 7 -18 8
0 3 10 -8
___________________
3 10 -8 0
Therefore the quadratic equation is
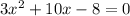
To find the factors of the above equation:
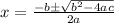
Where a and b are coefficients of
 and x respectively
and x respectively
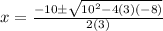 Where a=3 , b=10 and c=-8
Where a=3 , b=10 and c=-8
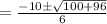
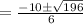
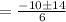
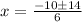
Therefore
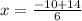 and
and
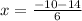
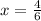 and
and
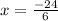
Therefore
 and
and
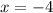
Therefore the factors are x-2,
 and x+4
and x+4