Question

the units digit of a two-digit number is twice the tens digit. If the digits are reversed, the new number is 9 less than the original number. What is the original number?

Answer 1

36

Explanation:

Here is the correct and complete question: The units digit of a two-digit number is twice the tens digit. If the digits are reversed, the new number is 9 less than twice the original number. What is the original number?

Lets assume the original number be"10y+x". (x is unit digit and y is 10th digit)

∴ if number is reversed then resulting number be "10x+y".

As given: x= 2y

and
`10x+y= 2(10y+x)-9`

Now, solving the equation to get original number.

`10x+y= 2(10y+x)-9`

Distributing 2 to 10y and x, then opening the parenthesis.

⇒
`10x+y= 20y+2x-9`

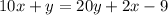
subtracting by (2x+y) on both side.

⇒
`8x= 19y-9`

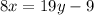
subtituting the value of "x", which is equal to 2y.

∴
`8* 2y= 19y-9`

⇒
`16y=19y-9`

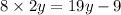
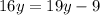
subtracting both side by (16y-9)

⇒
`3y= 9`

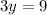
cross multiplying

We get,
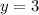
`y= 3`

y=3

∵x= 2y

`x=2* 3= 6`

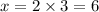
∴ x= 6

Therefore, the original number will be 36 as x is the unit number and y as tenth number.