Question

The population of deer in a certain national park can be approximated by the function P(x)=150(1.07)^x, where x is the number of years since 1995. In which year will the population reach 300? Hint: an answer such as 2002.4 would represent the year 2002.

A.2026
B.2005
C.2038
D.2016

Answer 1

b. 2005

Explanation:

(apex)

300=150(1.07)^x

1.07^x=2

x=ln 2/ln 1.07

=10.24

1995 plus ten years = 2005

hope this helps

Answer 2

B. 2005

Explanation:

We have been given that population of deer in a certain national park can be approximated by the function
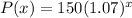`P(x)=150(1.07)^x`, where x is the number of years since 1995. We are asked to find the year in which population will reach 300.

To solve our given problem, we will equate
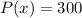`P(x)=300` and solve for x as:

`300=150(1.07)^x`

`(300)/(150)=(150(1.07)^x)/(150)`

`2=(1.07)^x`

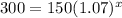
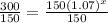
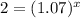
Now, we will take natural log on both sides as:

`\text{ln}(2)=\text{ln}((1.07)^x)`

`\text{ln}(2)=x\text{ln}(1.07)`

`x=\frac{\text{ln}(2)}{\text{ln}(1.07)}`

`x=10.2447`

`x\approx 10`

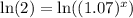
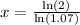
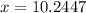
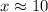
Now, we will find 10 years after 1995 that is
`1995+10=2005`.

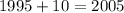Therefore, the population will be 300 in year 2005 and option B is the correct choice.