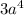Answer:
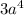
Explanation:
What is the cube root of
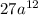 ? This is the question.
? This is the question.
We can write:
![\sqrt[3]{27a^(12)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kimqo5jna1ssazbnam673k829jmh7lvjsa.png)
We will use the below property to simplify:
![\sqrt[n]{a*b}=\sqrt[n]{a} \sqrt[n]{b}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/j9df1q7nen28ey0ikmw66alxdoxr8d8cq2.png)
So, we have:
![\sqrt[3]{27a^(12)} =\sqrt[3]{27} \sqrt[3]{a^(12)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/kd0t0jtm8eu2i14h6zyog8vmmgpmlsusf1.png)
We will now use below property to further simplify:
![\sqrt[n]{x} =x^{(1)/(n)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/jm768bjepgtuz2fktj03nc6o37fb41iqjk.png)
Thus, we have:
![\sqrt[3]{27} \sqrt[3]{a^(12)} =3*(a^(12))^{(1)/(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/o1wonrvzu6ylrlatoaa8f4u6u5a7w55nwk.png)
We know power to the power rule:
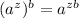
Now, we have:
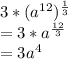
This is the correct answer: