Question

Find the relative minimum of

y = 3x^3 + 14x^2 - 11x - 46

(___ , ____)

Round your answers to the nearest tenth when applicable.

Write your answer in the format (a, b). ​

Answer 1

Explanation:

The max and min values exist where the derivative of the function is equal to 0. So we find the derivative:

`y'=9x^2+28x-11`

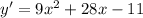
Setting this equal to 0 and solving for x gives you the 2 values

x = .352 and -3.464

Now we need to find where the function is increasing and decreasing. I teach ,my students to make a table. The interval "starts" at negative infinity and goes up to positive infinity. So the intervals are

-∞ < x < -3.464 -3.464 < x < .352 .352 < x < ∞

Now choose any value within the interval and evaluate the derivative at that value. I chose -5 for the first test number, 0 for the second, and 1 for the third. Evaluating the derivative at -5 gives you a positive number, so the function is increasing from negative infinity to -3.464. Evaluating the derivative at 0 gives you a negative number, so the function is decreasing from -3.464 to .352. Evaluating the derivative at 1 gives you a positive number, so the function is increasing from .352 to positive infinity. That means that there is a min at the x value of .352. I guess we could round that to the tenths place and use .4 as our x value. Plug .4 into the function to get the y value at the min point.

f(.4) = -48.0

So the relative min of the function is located at (.4, -48.0)