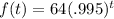Question

Find the exponential function that satisfies the given conditions: Initial value = 64, decreasing at a rate of 0.5% per week

f(t) = 0.5 ⋅ 0.36t

f(t) = 64 ⋅ 1.005t

f(t) = 64 ⋅ 0.995t

f(t) = 64 ⋅ 1.5t

Answer 1

f(t) = 64 ⋅ 0.995t

Explanation:

Add me on S n a p c h a t :) yofav_tai

Answer 2

Explanation:

An exponential function is of the form

`y=ab^x`

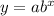
where a is the initial value and b is the growth/decay rate. Our initial value is 64. That's easy to plug in. It goes in for a. So the first choice is out. Considering b now...

If the rate is decreasing at .5% per week, this means it still retains a rate of

100% - .5% = 99.5%

which is .995 in decimal form.

b is a rate of decay when it is greater than 0 but less than 1; b is a growth rate when it is greater than 1. .995 is less than 1 so it is a rate of decay. The exponential function is, in terms of t,

`f(t) = 64(.995)^t`