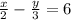Question

The sum of two consecutive numbers is 77. The difference of half of the smaller number and one-third of the larger number is 6. If x is the smaller number and y is the larger number, which two equations represent the sum and difference of the numbers? x - y = 6 and 1/2 x + 1/3 y = 77 x + y = 77 and 1/2 x - 1/3 y = 6 x - y = 77 and 1/2 x + 1/3 y = 6

Answer 1

The required equations that represent the sum and difference of numbers are: x + y = 77 and
`(x)/(2) - (y)/(3) = 6`

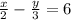
Solution:

Let the two consecutive numbers be "x" and "y"

Where "x" is the smaller number and "y" is the larger number

Given that sum of two consecutive numbers is 77

Therefore we frame a equation as:

x + y = 77

Also given that The difference of half of the smaller number and one-third of the larger number is 6

Therefore we frame a equation as:

half of the smaller number - one-third of the larger number = 6

half of x - one third of y = 6

`(1)/(2)x - (1)/(3)y = 6\\\\(x)/(2) - (y)/(3) = 6`

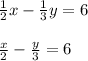
Therefore the required equations that represent the sum and difference of numbers are:

x + y = 77

`(x)/(2) - (y)/(3) = 6`