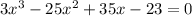Question

Create an equation where the solutions are 1/3 and 4 plus or minus i sqrt 7

Answer 1

`3 {x}^(3) - 25 {x}^(2) + 35x - 23 = 0`

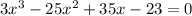
Explanation:

We want to create an equation that will have the solution

`x = (1)/(3),x = 4 + √(7)i,x = 4 - √(7)i`

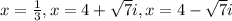
This implies that:

`3x -1= 0,x -( 4 + √(7)i) = 0,x - ( 4 - √(7)i) = 0`

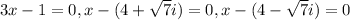
We put the roots in factored form by reversing the zero product principle to get:

`(3x -1)(x -( 4 + √(7)i))(x - ( 4 - √(7)i)) = 0`

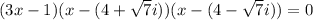
We expand the last two parenthesis to get:

`(3x - 1)( {x}^(2) - 4x + √(7)ix - 4x - √(7)ix + 16 - 7 {i}^(2)) = 0`

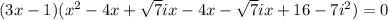
We simplify to get:

`(3x - 1)( {x}^(2) - 8x + 23) = 0`

We expand further to obtain:

`3 {x}^(3) - 25 {x}^(2) +35x - 23 = 0`