Answer:
Option E) is correct.
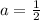
Explanation:
Given trignometric equation is
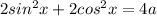
To find the value of "a" from the given equation:
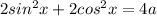
Taking common number "2" outside the equation of left hand side
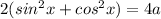


( We know the trignometric formula
 here
here
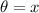 )
)
Therefore
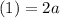

It can be written as
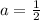
Therefore
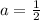
Option E) is correct.