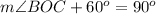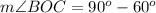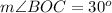2 Answers

Zsljulius · Answer 1 · 2021-05-15T22:50:59+0000

Answer:

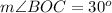
$m\angle BOC=30^o$

Explanation:

step 1

Find the measure of angle COD

we know that

$m\angle COF=m\angle COD+m\angle DOF$ ---> by addition angle postulate

we have

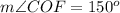$m\angle COF=150^o$ ----> given problem

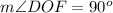$m\angle DOF=90^o$ ----> because AD is perpendicular to BF

substitute the given values

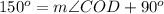
$150^o=m\angle COD+90^o$

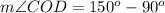
$m\angle COD=150^o-90^o$

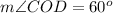
$m\angle COD=60^o$

step 2

Find the measure of angle BOC

we know that

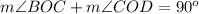$m\angle BOC+m\angle COD=90^o$ ---> by complementary angles

we have

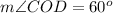
$m\angle COD=60^o$

substitute

$m\angle BOC+60^o=90^o$

$m\angle BOC=90^o-60^o$

$m\angle BOC=30^o$

Please log in or register to add a comment.