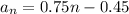Question

What is the closed linear form for this sequence given a1 = 0.3 and an + 1 = an + 0.75?

Answer 1

The closed linear form of the given sequence is
`a_(n)=0.75n-0.45`

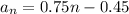
Explanation:

Given that the first term
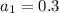`a_(1)=0.3` and
`a_(n+1)=a_(n)+0.75`

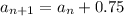
To find the closed linear form for the given sequence

The formula for arithmetic sequence is

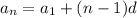`a_(n)=a_(1)+(n - 1)d` (where d is the common difference)

The above equation is of the given form
`a_(n+1)=a_(n)+0.75`

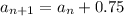
Comparing this we get d=0.75

With
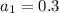`a_(1)=0.3` and d=0.75

We can substitute these values in
`a_(n)=a_(1)+(n - 1)d`

`a_(n)=a_(1)+(n - 1)d`

`=0.3+(n-1)(0.75)`

`=0.3+0.75n-0.75`

`=-0.45+0.75n`

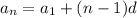
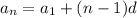
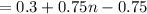
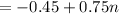
Rewritting as below

`=0.75n-0.45`

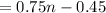
Therefore
`a_(n)=0.75n-0.45`

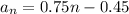
Therefore the closed linear form of the given sequence is
`a_(n)=0.75n-0.45`