Answer:
See the explanation.
Explanation:
Given function
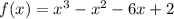
And the interval
![[0,3]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/malesjs1vrtvz6jkw79g2w1n8o6j5taznh.png)
According to Rolle's Theorem
Let
 be differentiable on the open interval
be differentiable on the open interval
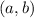 and continuous on the closed interval
and continuous on the closed interval
![[a,b]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dyyh30s5r4ox0wg76shisxuulr9zptlacg.png) . Then if
. Then if
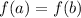 , then there is at least one point
, then there is at least one point
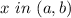 where
where
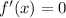 .
.
So,
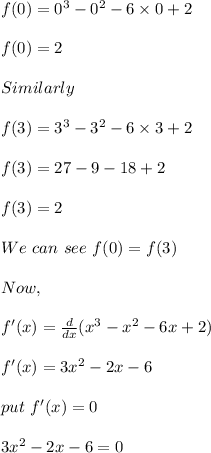
We will find the value of
 for which
for which
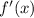 became zero.
became zero.
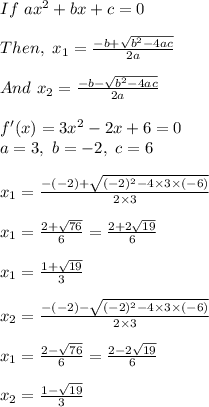
We can see
![x_(1)=(1+√(19))/(3)=1.786\\\\and\ 1.786\ is\ in\ [0,3]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/288mcy8bl22vrvdlr22jgz8ejzu2phu8uf.png)
There is at least one point
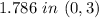 where
where
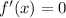 .
.