The statements which are true are:
(6, 6) is the midpoint of CD
(4, 3) is the intersection point of diagonals of parallelogram
Solution:
The mid point (x,y) =
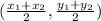
Midpoint of AB
A(-2, -1) and B(6, 1)
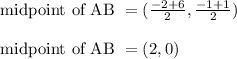
Thus statement 1 is wrong
Midpoint of BC
B(6, 1) and C(10, 7)
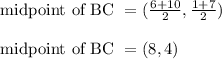
Thus statement 2 is wrong
Mid point of CD
Here ,
 = 10
= 10
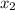 = 2
= 2
 = 7
= 7
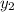 =5
=5
now substituting these values,
mid point of CD =
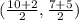
mid point of CD =
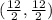
mid point of CD =
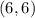
Therefore (6, 6) is the midpoint of CD
Statement 3 is correct
Midpoint of AD
A = (-2, -1) and D = (2, 5)
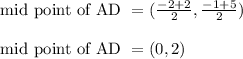
Thus statement 4 is wrong
Intersection point of diagonals of parallelogram
Let AC and BD be the diagonals of parallelogram
The diagonals of a parallelogram bisect each other, therefore, the point of intersection is the midpoint of either.
Midpoint of AC:
A = (-2, -1) and C(10, 7)
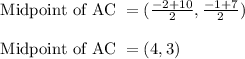
Thus statement 5 is correct