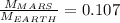Answer: 0.107
Step-by-step explanation:
We can solve this problem with Kepler's Third Law of Planetary motion:
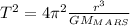 (1)
(1)
Where:
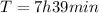 is the orbital period of Phobos around Mars
is the orbital period of Phobos around Mars
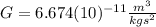 is the Gravitational Constant
is the Gravitational Constant
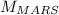 is the mass of Mars
is the mass of Mars
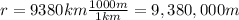 is the semimajor axis of the orbit Phobos describes around Mars (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
is the semimajor axis of the orbit Phobos describes around Mars (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit)
Well, firstly we have to convert the orbital period to seconds:
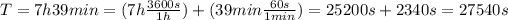
Now, we have to find
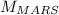 from (1):
from (1):
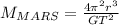 (2)
(2)
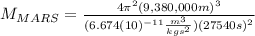 (3)
(3)
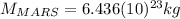 (4) This is the mass of Mars
(4) This is the mass of Mars
On the other hand, it is known the mass of the Earth is:
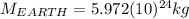 (5)
(5)
Then, if we want to know the ratio of Mars’s mass to the mass of the earth, we have to divide
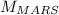 by
by
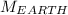 :
:
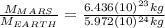
Finally: