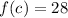Question

NEED HELP PLEASE I HAVE 6 DAYS TO COMPLETE EVERYTHING

Answer 1

C. 4

Explanation:

f(c) = 28 = 2x² - 4

28 = 2x² - 4

32 = 2x²

16 = x²

±4 = x

x = 4

c = 4

Answer 2

Option c) is correct

ie., c=4 represents the value of c suchthat function
`f(c)=28`

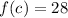
Explanation:

Given function f is defined by
`f(x)=2x^(2)-4`

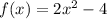
To find the value of "c" such that
`f(c)=28`

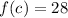
Therefore put x=c in the given function as

`f(x)=2x^(2)-4`

`f(c)=2c^(2)-4`

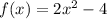
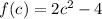
and we have
`f(c)=28`

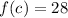
Now equating the two functions

`f(c)=2c^(2)-4=28`

`2c^(2)-4=28`

`2c^(2)=28+4`

`c^(2)=(32)/(2)`

`c^(2)=16`

`c=4`

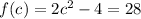
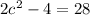
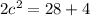
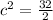
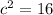
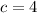
Therefore
`c=4`

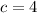
Option c) is correct

ie., c=4 represents the value of c suchthat function
`f(c)=28`