Question

A line containing the points (3,0) and (-2,-2) is graphed on a coordinate grid. Which of these

points is a solution to the equation that represents this line?

(-12,-6)
(-4,-3)
(0.5,-1)
(5,0.8)
(9,3)
(18,6)

Answer 1

Answer: (-12,-6)

Explanation:

If we already have two points of the line, we can find its slope (
`m`), its intersection with the y-axis (
`b`), hence its equation:

Point 1:
`(x_(1),y_(1))=(3,0)`

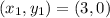
Point 2:
`(x_(2),y_(2))=(-2,-2)`

Slope equation:

`m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`m=(-2-0)/(-2-3)`

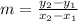
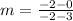
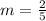`m=(2)/(5)` This is the slope of the line

Now, the equation of the line is:

`y=mx+b`

We already know the slope, now we have to find
`b` with any of the given points. Let's choose Point 1:
`(x_(1),y_(1))=(3,0)`

`0=(2)/(5)(3)+b`

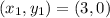
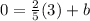
Isolating
`b`:

`b=-(6)/(5)`

Then, the equation of the line is:

`y=(2)/(5) x-(6)/(5)`

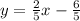
With this equation we can find which point is a solution. Let's begin with the first point (-12,-6):

`-6=(2)/(5) (-12)-(6)/(5)`

`-6=-(24)/(5) -(6)/(5)`

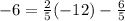
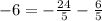
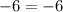`-6=-6` Since both sides of the equation are equal, (-12,-6) is the point that fulfills the solution of the equation.