Question

Can you explain these questions and how you got the answers?

Answer 1

B

A

Explanation:

`f(x) = \left \{ \left \begin{matrix}5x-6,\ x<4\\x^(2)-2,\ 4 \leq x \leq 6\\4x+10,\ x>6 \end{matrix} \right } \right`

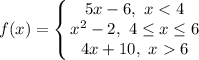
To find f'(x), take the derivative within each interval. Clearly, it's 5 in the first one, 2x in the second one, and 4 in the third one. But we need to determine if the derivative exists at the ends of each interval.

For a derivative to exist at a point x=a, the function must be continuous (f(a⁻) = f(a⁺)), and smooth (f'(a⁻) = f'(a⁺)).

Let's look at x=4. On the left side:

f(4⁻) = 14, f'(4⁻) = 5

On the right side:

f(4⁺) = 14, f'(4⁺) = 8

So the function is continuous, but not smooth. Therefore, the derivative doesn't exist there.

Let's try again with x=6. On the left side:

f(6) = 34, f'(6) = 12

On the right side:

f(6⁺) = 34, f'(6⁺) = 4

Again, the function is continuous, but not smooth, so the derivative doesn't exist there either.

Therefore, f'(x) is:

`f'(x) = \left \{ \left \begin{matrix}5,\ x<4\\2x,\ 4<x<6\\4,\ x>6 \end{matrix} \right } \right\ Domain:\ All\ real\ numbers,\ x\\eq 4,6`

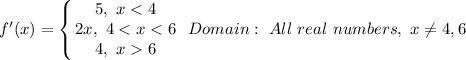
When we graph f(x) = (4x² − 1) / (x² − 9), we see f(x) has a horizontal tangent line at x=0.

desmos.com/calculator/6y3r1ju7jx