Question

The first three terms of a sequence are given. Round to the nearest thousandth (if necessary).

100
,
80
,
64
,
.
.
.
100,80,64,...
Find the 9th term.
Find the

Answer 1

The 9th term for given sequence is 16.777

Therefore the 9th term is
`a_(9)=16.777`.

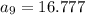Explanation:

Given first three terms of a sequence are 100,80,64,...

Given
`a_(1)=100` ,
`a_(2)=80` ,
`a_(3)=64`,...

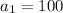Given sequence is of the form of Geometric sequence

Therefore it can be written as
`{\{a,ar,ar^2,...}\}`

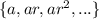
therefore a=100 , ar=80 ,
`ar^2=64` ,...

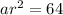To find common ratio

`r=(a_(2))/(a_(1))`

`r=(80)/(100)`

`r=(4)/(5)`

`r=(a_(3))/(a_(2))`

`r=(64)/(80)`

`r=(4)/(5)`

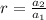
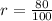
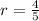
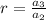
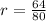
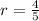
Therefore
`r=(4)/(5)`

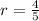
The nth term of the geometric sequence is

`a_(n)=ar^(n-1)`

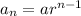
To find the 9th tem for the given geometric sequence is

`a_(n)=ar^(n-1)`

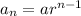
put n=9, a=100 and
`r=(4)/(5)`

`a_(9)=100((4)/(5))^(9-1)`

`=100((4)/(5))^(8)`

`=100((4)/(5)* (4)/(5)* (4)/(5)* (4)/(5)* (4)/(5)* (4)/(5)* (4)/(5)* (4)/(5))`

`=100((256* 256)/(625* 625))`

`=100((65536)/(390625))`

`=100(0.16777})`

`=16.777`

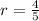
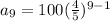
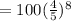
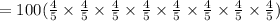
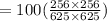
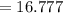
Therefore
`a_(9)=16.777`

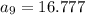
The 9th term is 16.777