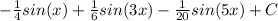Question

Find ∫sin²x cos3x dx​

Answer 1

`-(1)/(4) sin(x)+(1)/(6) sin(3x)-(1)/(20) sin(5x)+C`

Explanation:

We begin with the integral
`\int{sin^2(x)cos(3x)} \, dx`

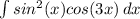
First, we can apply the power reducing formula to
`sin^2(x)`

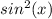
This formula states:
`sin^2(x)=(1)/(2) -(1)/(2) cos(2x)`

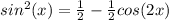
This gives us

`\int{((1)/(2) -(1)/(2) cos(2x))(cos(3x)} \, dx \\\\\int{((1)/(2)cos(3x) -((1)/(2) cos(2x)cos(3x)} \, dx \\\\(1)/(2) \int{cos(3x)} \, dx -(1)/(2) \int{cos(2x)cos(3x)} \, dx`

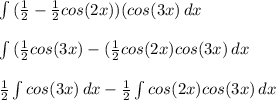
Now, we can use integrate the first integral

`(1)/(2) \int{cos(3x)} \, dx\\u=3x\\du=3dx\\\\(1)/(6) \int{3cos(u)} \, du\\\\(1)/(6) sin(u)+C\\\\(1)/(6) sin(3x)+C`

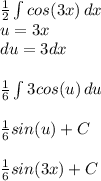
And now we can begin to integrate the second

`-(1)/(2) \int{cos(2x)cos(3x)} \, dx`

To integrate this, we need to use the Product-to-sum formula, which states

`cos(\alpha )cos(\beta )=(1)/(2) [cos(\alpha +\beta )+cos(\alpha -\beta )` . For this formula, we will use
`\alpha =3x\\\beta =2x`

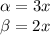
This gives us

`-(1)/(2) \int{(1)/(2)[cos(5x)+cos(x)] } \, dx \\\\-(1)/(4) \int{[cos(5x)+cos(x)] } \, dx\\\\-(1)/(4)\int{cos(5x)} \, dx -(1)/(4)\int{cos(x)} \, dx`

We can then use the same process of u-substitution as the previous to get the answer of
`-(1)/(20) sin(5x)-(1)/(4) sin(x)+C`

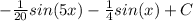
Lastly, we can add the values of the two integrals together to give us the final solution of

`-(1)/(4) sin(x)+(1)/(6) sin(3x)-(1)/(20) sin(5x)+C`